Thermal Transport from HNEMD

Introduction

In this tutorial, we use the HNEMD method to study heat transport in graphene at 300 K and zero pressure. Here we consider the diffusive regime. The ballistic regime can be found in the NEMD example. The spectral decomposition method as described in [Fan 2019] is used here.

Importing Relevant Functions

The inputs/outputs for GPUMD are processed using the Atomic Simulation Environment (ASE).

from pylab import *
from ase.build import graphene_nanoribbon
from ase.io import write
from scipy.integrate import cumtrapz

Preparing the Inputs

We consider a graphene sheet of size of about 25 nm x 25 nm (24000 atoms). The transport is in the \(y\) direction. We divide the length in the \(y\) direction into 2 groups, with 4000 atoms in group 0 and 20000 atoms in group 1 We use a Tersoff-style potential (Tersoff (1989)) parameterized by Lindsay et al. [Lindsay 2010].

Generate the model.xyz file:

gnr =  graphene_nanoribbon(100, 60, type='armchair', sheet=True, vacuum=3.35/2)
gnr.euler_rotate(theta=90)
l = gnr.cell.lengths()
gnr.cell = gnr.cell.new((l[0], l[2], l[1]))
l = l[2]
gnr.center()
gnr.pbc = [True, True, False]
gnr

Atoms(symbols='C24000', pbc=[True, True, False], cell=[245.95121467478057, 255.6, 3.35])

Add Groups

Ly = 3*1.42*10
split = [0, Ly, 255.6]

group_label = np.zeros(len(gnr))
for i, atom in enumerate(gnr):
    y_pos = atom.position[1]
    for j in range(len(split)):
        if y_pos > split[j] and y_pos < split[j+1]:
            group_label[i] = j

gnr.arrays["group"] = np.array(group_label)

for i in range(len(split)-1):
    atom_num = len(gnr[gnr.arrays["group"] == i])
    print(f"group {i}: {atom_num} atoms")

group 0: 4000 atoms
group 1: 20000 atoms

write("model.xyz", gnr)

The run.in file:

The run.in input file is given below:

potential    ../../../../potentials/tersoff/Graphene_Lindsay_2010_modified.txt
velocity     300

ensemble     nvt_nhc 300 300 100
time_step    1
dump_thermo  1000
run          1000000

ensemble      nvt_nhc 300 300 100
compute_hnemd 1000 0 0.00001 0
compute_shc   2 250 1 1000 400.0 group 0 0
run           10000000

The first line uses the potential keyword to define the potential to be used, which is specified in the file Graphene_Lindsay_2010_modified.txt.

The second line uses the velocity keyword and sets the velocities to be initialized with a temperature of 300 K.

There are two runs. The first run serves as the equilibration stage.

• Here, the NVT ensemble (the Nose-Hoover chain thermostat) is used. The target temperature is 300 K and the thermostat coupling constant is 0.1 ps (100 time steps).

• The time_step for integration is 1 fs.

• The thermodynamic quantities will be output every 1000 steps.

• There are \(10^6\) steps (1 ns) for this run.

• The second run is for production.

  • Here, the global temperature is controlled by the Nose-Hoover chain thermostat (ensemble) with the same parameters as in the equilibration stage.

  • The compute_hnemd is used to add a driving force and compute the thermal conductivity using the HNEMD method [Fan 2019]. Here, the conductivity data will be averaged for each 1000 steps before written out, and the driving force parameter is \(10^{-5}\) A-1 and is in the \(y\) direction.

  • The line with the compute_shc keyword is used to compute the spectral heat current (SHC). The SHC will be calculated for group 0 in grouping method 0. The relevant data will be sampled every 2 steps and the maximum correlation time is \(250 \times 2 \times 1~{\rm fs} = 500~{\rm fs}\). The transport directions is 1 (\(y\) direction). The number of frequency points is 1000 and the maximum angular frequncy is 400 THz.

  • There are \(10^7\) steps (10 ns) in the production run. This is just an example. To get more accurate results, we suggest you use \(2 \times 10^7\) steps (20 ns) and do a few independent runs and then average the relevant data.

Results and Discussion

Computation Time

Using a GeForce RTX 2080 Ti GPU, the HNEMD simulation takes about 1.5 hours.

Figure Properties

aw = 2
fs = 16
font = {'size'   : fs}
matplotlib.rc('font', **font)
matplotlib.rc('axes' , linewidth=aw)

def set_fig_properties(ax_list):
    tl = 8
    tw = 2
    tlm = 4

    for ax in ax_list:
        ax.tick_params(which='major', length=tl, width=tw)
        ax.tick_params(which='minor', length=tlm, width=tw)
        ax.tick_params(which='both', axis='both', direction='in', right=True, top=True)

Plot HNEMD Results

The kappa.out output file is loaded and processed to create the following figure.

labels_kappa = ['kxi', 'kxo', 'kyi', 'kyo', 'kz']
kappa_array = np.loadtxt("kappa.out")

kappa = dict()
for label_num, key in enumerate(labels_kappa):
    kappa[key] = kappa_array[:, label_num]

def running_ave(y, x):
    return cumtrapz(y, x, initial=0) / x

t = np.arange(1,kappa['kxi'].shape[0]+1)*0.001  # ns
kappa['kyi_ra'] = running_ave(kappa['kyi'],t)
kappa['kyo_ra'] = running_ave(kappa['kyo'],t)
kappa['kxi_ra'] = running_ave(kappa['kxi'],t)
kappa['kxo_ra'] = running_ave(kappa['kxo'],t)
kappa['kz_ra'] = running_ave(kappa['kz'],t)

figure(figsize=(12,10))
subplot(2,2,1)
set_fig_properties([gca()])
plot(t, kappa['kyi'],color='C7',alpha=0.5)
plot(t, kappa['kyi_ra'], linewidth=2)
xlim([0, 10])
gca().set_xticks(range(0,11,2))
ylim([-2000, 4000])
gca().set_yticks(range(-2000,4001,1000))
xlabel('time (ns)')
ylabel(r'$\kappa_{in}$ W/m/K')
title('(a)')

subplot(2,2,2)
set_fig_properties([gca()])
plot(t, kappa['kyo'],color='C7',alpha=0.5)
plot(t, kappa['kyo_ra'], linewidth=2, color='C3')
xlim([0, 10])
gca().set_xticks(range(0,11,2))
ylim([0, 4000])
gca().set_yticks(range(0,4001,1000))
xlabel('time (ns)')
ylabel(r'$\kappa_{out}$ (W/m/K)')
title('(b)')

subplot(2,2,3)
set_fig_properties([gca()])
plot(t, kappa['kyi_ra'], linewidth=2)
plot(t, kappa['kyo_ra'], linewidth=2, color='C3')
plot(t, kappa['kyi_ra']+kappa['kyo_ra'], linewidth=2, color='k')
xlim([0, 10])
gca().set_xticks(range(0,11,2))
ylim([0, 4000])
gca().set_yticks(range(0,4001,1000))
xlabel('time (ns)')
ylabel(r'$\kappa$ (W/m/K)')
legend(['in', 'out', 'total'])
title('(c)')


subplot(2,2,4)
set_fig_properties([gca()])
plot(t, kappa['kyi_ra']+kappa['kyo_ra'],color='k', linewidth=2)
plot(t, kappa['kxi_ra']+kappa['kxo_ra'], color='C0', linewidth=2)
plot(t, kappa['kz_ra'], color='C3', linewidth=2)
xlim([0, 10])
gca().set_xticks(range(0,11,2))
ylim([0, 4000])
gca().set_yticks(range(-2000,4001,1000))
xlabel('time (ns)')
ylabel(r'$\kappa$ (W/m/K)')
legend(['yy', 'xy', 'zy'])
title('(d)')

tight_layout()
show()

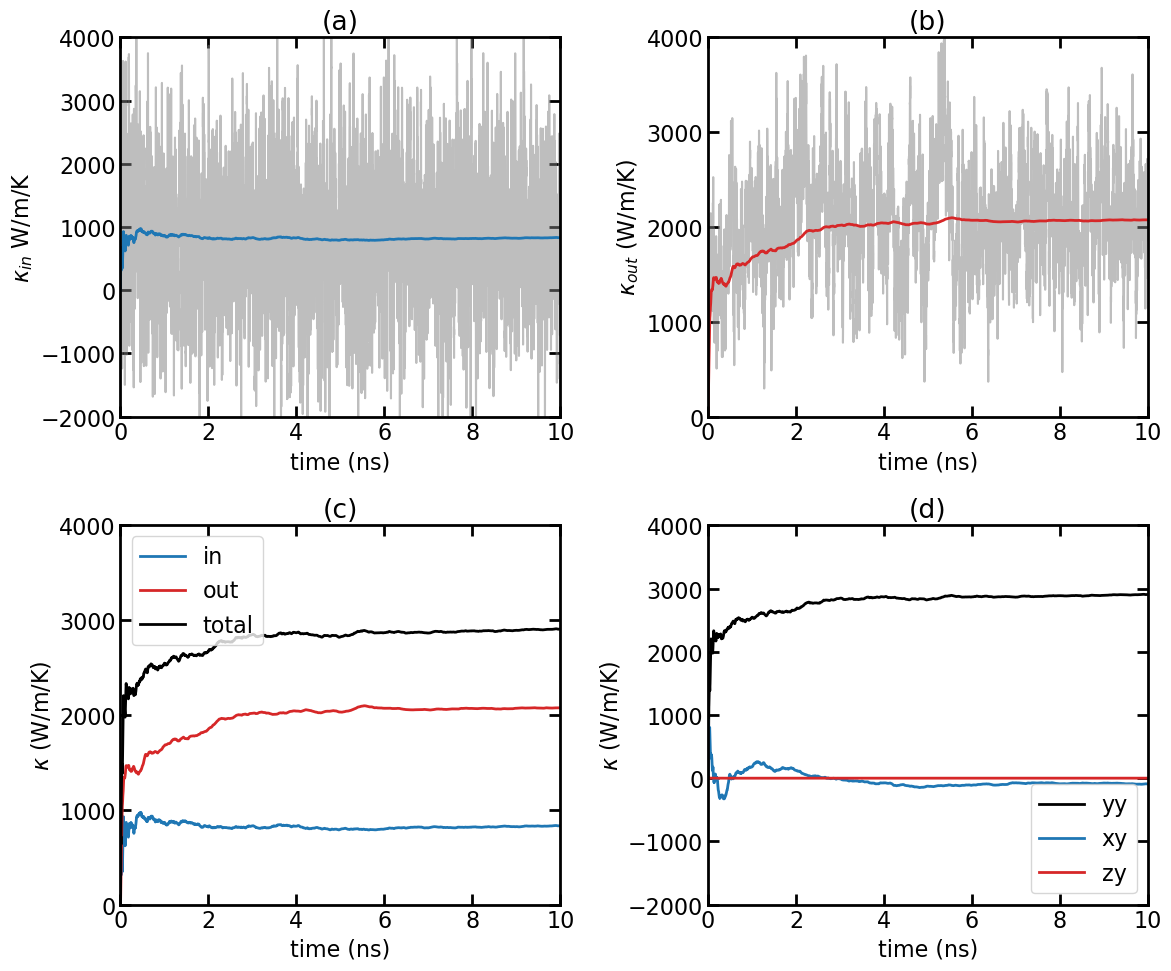
(a) In-plane thermal conductivity \(\kappa_{\rm in}(t)\) as a function of production time. (b) Out-of-plane thermal conductivity \(\kappa_{\rm out}(t)\) as a function of production time. (c) In-plane, out-of-plane, and total thermal conductivity as a function of production time. (d) Comparing \(\kappa_{yy}\), \(\kappa_{xy}\), and \(\kappa_{zy}\).

• 1. The gray line represents the instant in-plane thermal conductivity \(\kappa_{\rm in}(t)\) from the kappa.out file. The dashed line represents the cumulative time average:

     \[\kappa^{\rm ave}_{\rm in}(t) = \frac{1}{t} \int_0^t \kappa_{\rm in}(t') dt'\]

• 2. Similar to (a), but for the out-of-plane thermal conductivity \(\kappa_{\rm out}(t)\) and \(\kappa^{\rm ave}_{\rm out}(t)\).

• 3. Cumulative time averaged in-plane, out-of-plane, and total thermal conductivity: \(\kappa^{\rm ave}_{\rm in}(t)\), \(\kappa^{\rm ave}_{\rm out}(t)\) and \(\kappa^{\rm ave}_{\rm total}(t) = \kappa^{\rm ave}_{\rm in}(t) + \kappa^{\rm ave}_{\rm out}(t)\). It is clear that the out-of-plane phonons have a much large average phonon relaxation time (scattering time) than the in-plane phonons, and the thermal conductivity in pristine graphene is dominated by out-of-plane (flexural) phonons. This is consistent with the results from the EMD simulation as discussed in the EMD tutorial.

• 4. Some cumulative time averaged thermal conductivity components of the tensor: \(\kappa^{\rm ave}_{yy}(t)\), \(\kappa^{\rm ave}_{xy}(t)\) and \(\kappa^{\rm ave}_{zy}(t)\). It is clear that the off-diagonal components of the thermal conductivity tensor are zero.

Plot Spectral Heat Current Results

The shc.out output file is loaded and processed to create the following figure.

num_corr_points, num_omega = 250, 1000

labels_corr = ['t', 'Ki', 'Ko']
labels_omega = ['omega', 'jwi', 'jwo']

num_corr_points_in_run = num_corr_points * 2 - 1
coor_array = np.loadtxt("shc.out", max_rows=num_corr_points_in_run)
omega_array = np.loadtxt("shc.out", skiprows=num_corr_points_in_run)

shc = dict()
for label_num, key in enumerate(labels_corr):
    shc[key] = coor_array[:, label_num]

for label_num, key in enumerate(labels_omega):
    shc[key] = omega_array[:, label_num]
shc["nu"] = shc["omega"] / (2*np.pi)

shc.keys()

dict_keys(['t', 'Ki', 'Ko', 'omega', 'jwi', 'jwo', 'nu'])

def calc_spectral_kappa(shc, driving_force, temperature, volume):
    # ev*A/ps/THz * 1/A^3 *1/K * A ==> W/m/K/THz
    convert = 1602.17662
    shc['kwi'] = shc['jwi'] * convert / (driving_force * temperature * volume)
    shc['kwo'] = shc['jwo'] * convert / (driving_force * temperature * volume)


l = gnr.cell.lengths()
Lx, Lz = l[0], l[2]
V = Lx * Ly * Lz
T = 300
Fe = 1.0e-5
calc_spectral_kappa(shc, driving_force=Fe, temperature=T, volume=V)
shc['kw'] = shc['kwi'] + shc['kwo']
shc['K'] = shc['Ki'] + shc['Ko']
Gc = np.load('Gc.npy')
shc.keys()

dict_keys(['t', 'Ki', 'Ko', 'omega', 'jwi', 'jwo', 'nu', 'kwi', 'kwo', 'kw', 'K'])

lambda_i = shc['kw']/Gc
length = np.logspace(1,6,100)
k_L = np.zeros_like(length)
for i, el in enumerate(length):
    k_L[i] = np.trapz(shc['kw']/(1+lambda_i/el), shc['nu'])

figure(figsize=(12,10))
subplot(2,2,1)
set_fig_properties([gca()])
plot(shc['t'], shc['K']/Ly, linewidth=3)
xlim([-0.5, 0.5])
gca().set_xticks([-0.5, 0, 0.5])
ylim([-1, 5])
gca().set_yticks(range(-1,6,1))
ylabel('K (eV/ps)')
xlabel('Correlation time (ps)')
title('(a)')

subplot(2,2,2)
set_fig_properties([gca()])
plot(shc['nu'], shc['kw'],linewidth=3)
xlim([0, 50])
gca().set_xticks(range(0,51,10))
ylim([0, 200])
gca().set_yticks(range(0,201,50))
ylabel(r'$\kappa$($\omega$) (W/m/K/THz)')
xlabel(r'$\nu$ (THz)')
title('(b)')

subplot(2,2,3)
set_fig_properties([gca()])
plot(shc['nu'], lambda_i,linewidth=3)
xlim([0, 50])
gca().set_xticks(range(0,51,10))
ylim([0, 6000])
gca().set_yticks(range(0,6001,1000))
ylabel(r'$\lambda$($\omega$) (nm)')
xlabel(r'$\nu$ (THz)')
title('(c)')

subplot(2,2,4)
set_fig_properties([gca()])
semilogx(length/1000, k_L,linewidth=3)
xlim([1e-2, 1e3])
ylim([0, 3000])
gca().set_yticks(range(0,3001,500))
ylabel(r'$\kappa$ (W/m/K)')
xlabel(r'L ($\mu$m)')
title('(d)')

tight_layout()
show()

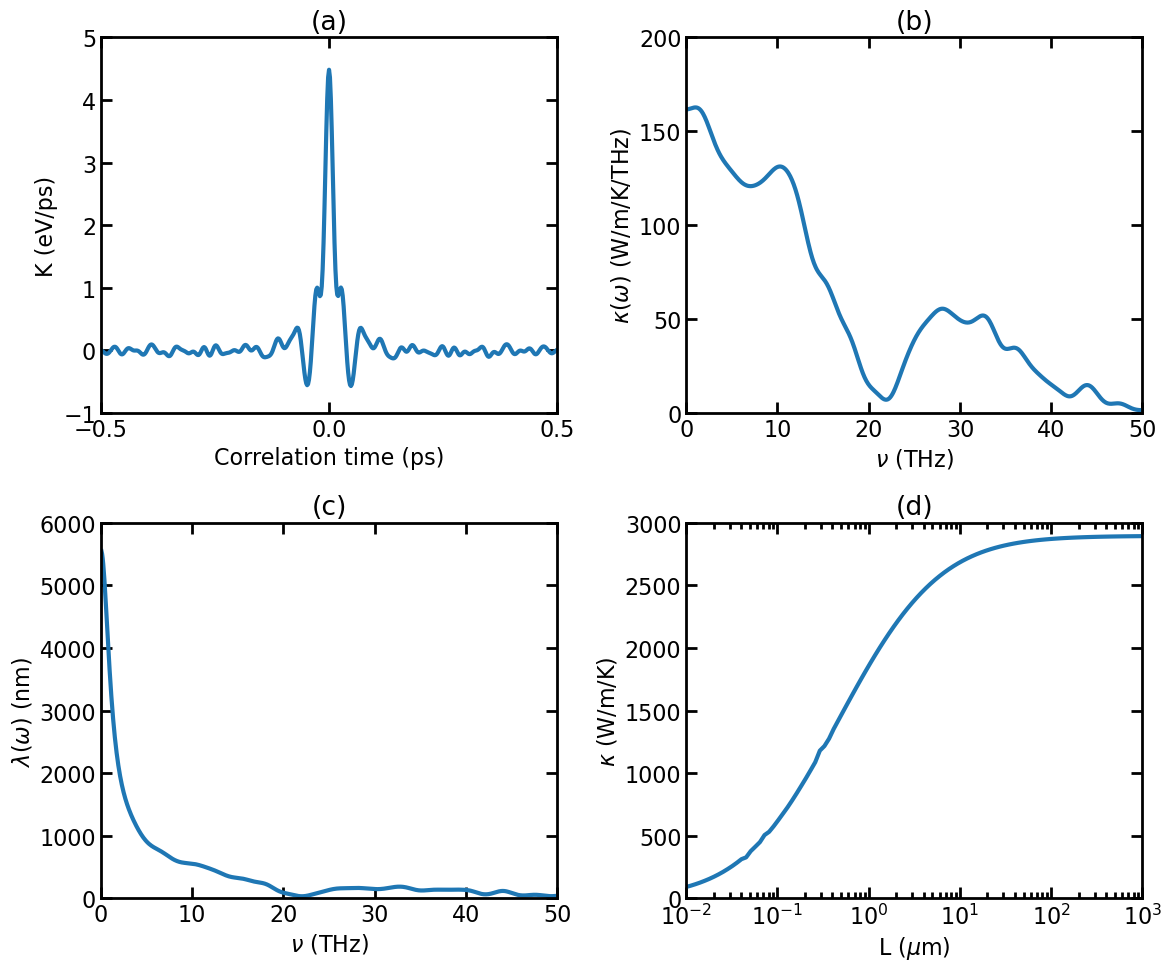
(a) Virial-velocity correlation function \(K(t)\). (b) Spectral thermal conductivity \(\kappa(\omega)\). (c) Spectral phonon mean free path \(\lambda(\omega)\). (d) Length-dependent thermal conductivity \(\kappa(L)\).

• The above figure shows the results from the HNEMD simulation [Fan 2019].

  • 1. The virial-velocity correlation function \(K(t)\). See Theoretical formulations for the definition of this quantity.

  • 2. The spectral thermal conductivity \(\kappa(\omega)\). See Theoretical formulations for the definition of this quantity.

  • 3. The spectral phonon mean free path calculated as [Fan 2019]

       \[\lambda(\omega)=\kappa(\omega)/G(\omega),\]

       where \(G(\omega)\) is the quasi-ballistic spectral thermal conductance from the above NEMD simulation.

  • 4. The length-dependent thermal conductivity calculated as [Fan 2019]

       \[\kappa(L) = \int \frac{d\omega}{2\pi} \frac{\kappa(\omega)}{1 + \lambda(\omega)/L}.\]

References

• [Fan 2019] Zheyong Fan, Haikuan Dong, Ari Harju, and Tapio Ala-Nissila, Homogeneous nonequilibrium molecular dynamics method for heat transport and spectral decomposition with many-body potentials, Phys. Rev. B 99, 064308 (2019).

• [Lindsay 2010] L. Lindsay and D.A. Broido, Optimized Tersoff and Brenner emperical potential parameters for lattice dynamics and phonon thermal transport in carbon nanotubes and graphene, Phys. Rev. B, 81, 205441 (2010).

• [Tersoff 1989] J. Tersoff, Modeling solid-state chemistry: Interatomic potentials for multicomponent systems, Phys. Rev. B 39, 5566(R) (1989).