Phonon Dispersion

Introduction

In this example, we use harmonic lattice dynamics to calculate the phonon dispersion of diamond silicon.

Importing Relevant Functions

The inputs/outputs for GPUMD are processed using the Atomic Simulation Environment (ASE) and the gpyumd package.

from pylab import *
from ase.build import bulk
from gpyumd.atoms import GpumdAtoms
from gpyumd.load import load_omega2

Preparting the Inputs

The structure as specified is 64-atom diamond silicon at zero temperature and zero pressure. We use the minimal Tersoff potential [Fan 2020].

Generate the model.xyz file:

Create Si Unit Cell & Add Basis

a=5.434
Si_UC = GpumdAtoms(bulk('Si', 'diamond', a=a))
Si_UC.add_basis()
Si_UC

GpumdAtoms(symbols='Si2', pbc=True, cell=[[0.0, 2.717, 2.717], [2.717, 0.0, 2.717], [2.717, 2.717, 0.0]])

Transform Si to Cubic Supercell

# Create 8 atom diamond structure
Si = Si_UC.repeat([2,2,1])
Si.set_cell([a, a, a])
Si.wrap()

# Complete full supercell
Si = Si.repeat([2,2,2])
Si

GpumdAtoms(symbols='Si64', pbc=True, cell=[10.868, 10.868, 10.868])

Write model.xyz File

write("model.xyz", Si)

Write basis.in File

• The basis.in file reads:

2
0 28
4 28
0
0
0
0
1
1
1
1
...

• Here the primitive cell is chosen as the unit cell. There are only two basis atoms in the unit cell, as indicated by the number 2 in the first line.

• The next two lines list the indices (0 and 4) and masses (both are 28 amu) for the two basis atoms.

• The next lines map all the atoms (including the basis atoms) in the super cell to the basis atoms: atoms equivalent to atom 0 have a label 0, and atoms equivalent to atom 1 have a label 1.

Note: The basis.in file generated by this Jupyter notebook may look different, but the same concepts apply and the results will be the same.

Si.write_basis()

Write kpoints.in File

• The \(k\) vectors are defined in the reciprocal space with respect to the unit cell chosen in the basis.in file.

• We use the \(\Gamma-X-K-\Gamma-L\) path, with 400 \(k\) points in total.

linear_path, sym_points, labels = Si_UC.write_kpoints(path='GXKGL',npoints=400)

The run.in file:

The run.in input file is given below:

potential       ../../../potentials/tersoff/Si_Fan_2019.txt
compute_phonon  5 0.005 # in units of A

• The first line with the potential keyword states that the potential to be used is specified in the file Si_Fan_2019.txt.

• The second line with the compute_phonon keyword tells that the force constants will be calculated with a cutoff of 5.0 \(\mathring A\) (here the point is that first and second nearest neighbors need to be included) and a displacement of 0.005 \(\mathring A\) will be used in the finite-displacement method.

Results and Discussion

Figure Properties

aw = 2
fs = 24
font = {'size'   : fs}
matplotlib.rc('font', **font)
matplotlib.rc('axes' , linewidth=aw)

def set_fig_properties(ax_list):
    tl = 8
    tw = 2
    tlm = 4

    for ax in ax_list:
        ax.tick_params(which='major', length=tl, width=tw)
        ax.tick_params(which='minor', length=tlm, width=tw)
        ax.tick_params(which='both', axis='both', direction='in', right=True, top=True)

Plot Phonon Dispersion

The omega2.out output file is loaded and processed to create the following figure. The previously defined kpoints are used for the \(x\)-axis.

nu = load_omega2()

figure(figsize=(10,10))
set_fig_properties([gca()])
vlines(sym_points, ymin=0, ymax=17)
plot(linear_path, nu, color='C0',lw=3)
xlim([0, max(linear_path)])
gca().set_xticks(sym_points)
gca().set_xticklabels([r'$\Gamma$','X', 'K', r'$\Gamma$', 'L'])
ylim([0, 17])
ylabel(r'$\nu$ (THz)')
show()

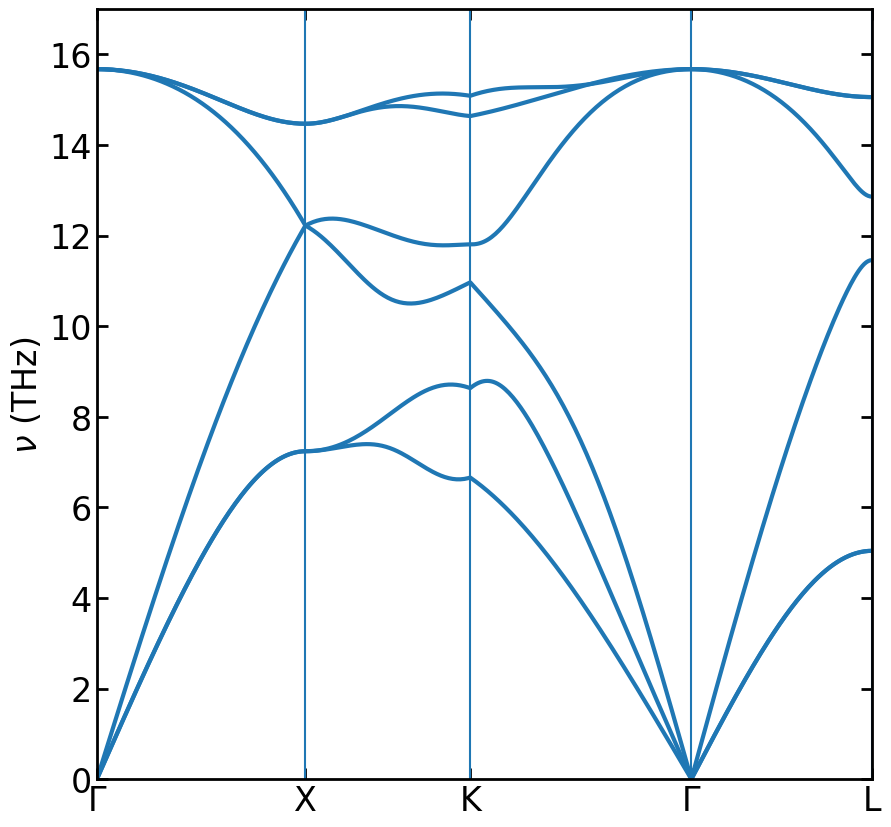
Phonon dispersion of silicon crystal described by the mini-Tersoff potential.

• The above figure shows the phonon dispersion of silicon crystal described by the mini-Tersoff potential [Fan 2020]

References

[Fan 2020] Zheyong Fan, Yanzhou Wang, Xiaokun Gu, Ping Qian, Yanjing Su, and Tapio Ala-Nissila, A minimal Tersoff potential for diamond silicon with improved descriptions of elastic and phonon transport properties, J. Phys.: Condens. Matter 32 135901 (2020).